 Исходя из требований психологической механики [1-2] дано определение "что есть Пространство" [3]. Исходя из требований психологической механики [1-2] дано определение "что есть Пространство" [3].
Пространство - это геометрия сред и отношений тел их обобщения, в котором разворачивается событие; изучение Геометрии осуществляется каверзным восприятием при резонансе токов orbitofrontal cortex лобной доли головного мозга [4], когда на основе человеческого ноумена составляется взаимное расположение форм и отношений тел или Пространств (не логикой разума).
Простейшие понятия Пространства
В геометрии [5-8]:
1) Расстояние s по кривой 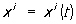 ( i = 1, …, n, 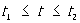 ) в пространстве определяется как интеграл
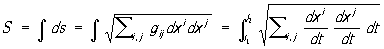
вдоль этой кривой.
2) Угол между двумя исходящими из одной точки А кривыми определяется как угол между касательными векторами к кривым в точке А.
3) Объём Vn-мерной области G пространства определяется по формуле:
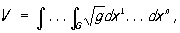 где где  . .
Эксперименты с пространством
На основе определения Пространства и каверзного восприятия при резонансе токов orbitofrontal cortex лобной доли головного мозга [4] проведем эксперименты с Геометрией:
Эксперимент. Реальное пространство является неоднородным
1. Различие расстояний между пунктами А и Б или пространство неоднородно. Напомним, в механике Ньютона пространство является однородным, когда две любые точки пространства неотличимы.
п 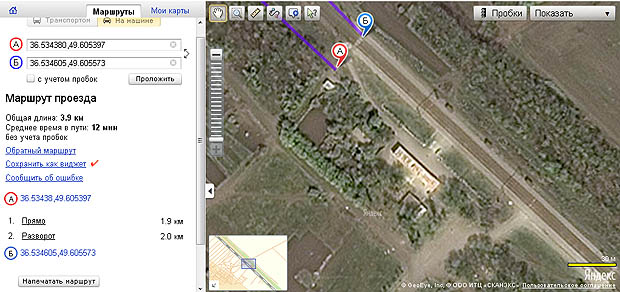
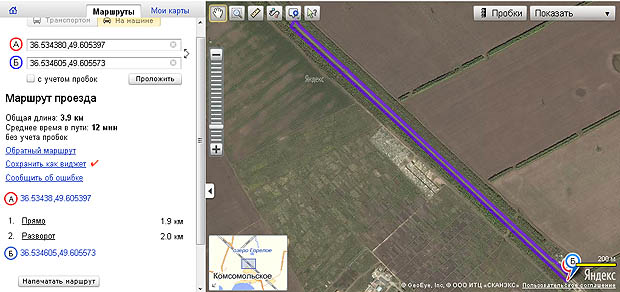
Южная ж.-д. Харьковской обл. Ос. "Комсомольская. Исходя из геометрии пространства для пешехода и велосипедиста расстояние между пунктами А и Б составляет 30 метров. Для легкового автомобиля (водителя) расстояние между теми же пунктами А и В составляет 2,0 км.
Эксперимент. Реальное пространство является анизотропным
2. Различие расстояний между пунктами А и Б или пространство является анизотропным. В механике Ньютона пространство является изотропным, когда два любых направления в пространстве неотличимы:
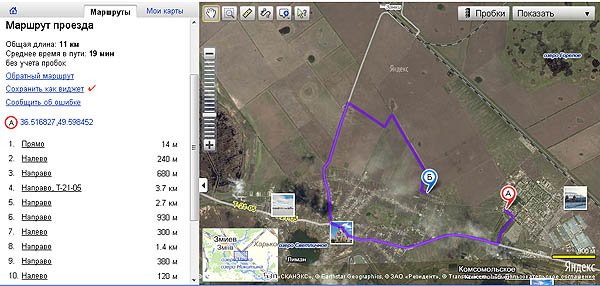
Карта п. Лиман и п. Комсомольское, Харьковской обл. Для легкового автомобиля (водителя) расстояние между пунктами А и Б составляет 11,0 км. В то время как для пешехода - 1,1 км и для велосипедиста - 350 м.
Эксперимент. Реальное пространство не является абсолютным
3. Различие расстояний между пунктами А и Б не является абсолютным. Напомним, пространство в механике Ньютона является абсолютным (не зависит от Наблюдателя):
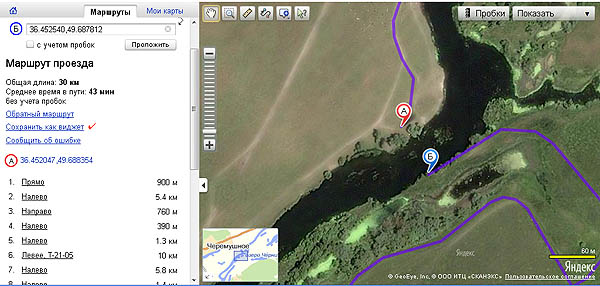
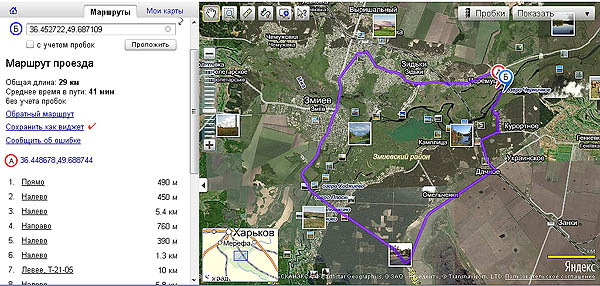
Карта участка р. Северский Донец между Дом Отдыха и п. Гинеевка, Харьковской обл. Для пловца и человека на плав. средстве расстояние между пунктами А и Б составляет 50 м. В то время как для автомобиля - 29 км; пешеход и велосипедист может воспользоваться электричкой, расстояние составит - 5 км
Эксперимент. Реальное пространство не является евклидовым и зависит от Наблюдателя
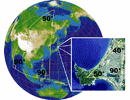
4. Круговая орбита станции МКС на географической карте Земли указывает на проблемы евклидова Пространства [9] классической механики Ньютона:
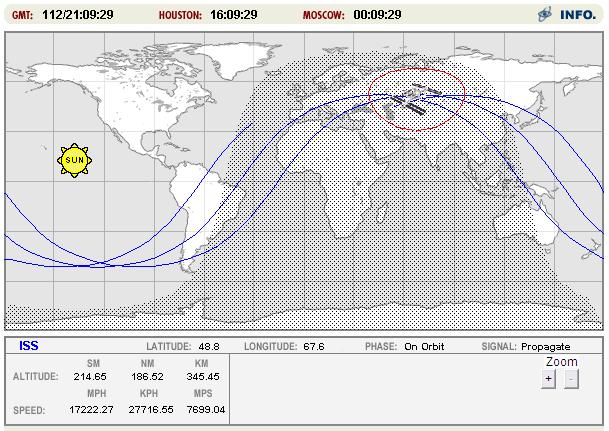
На иллюстрации можно увидеть местоположение МКС (Международной космической станции) в реальном времени на карте Земли. Карта местонахождения МКС
Эксперимент. Проблемы евклидова Пространства классической механики Ньютона
5. Геометрия Римана раскрывает проблемы евклидова Пространства [9] классической механики Ньютона:
Геометрия Римана и картография
Эксперимент. Движения космических аппаратов от Земли отличаются от световых линий
6. Эконом-траектории движения космических аппаратов от Земли к планетам Солнечной системы отличаются от визуальных (световых) линий между планетами:
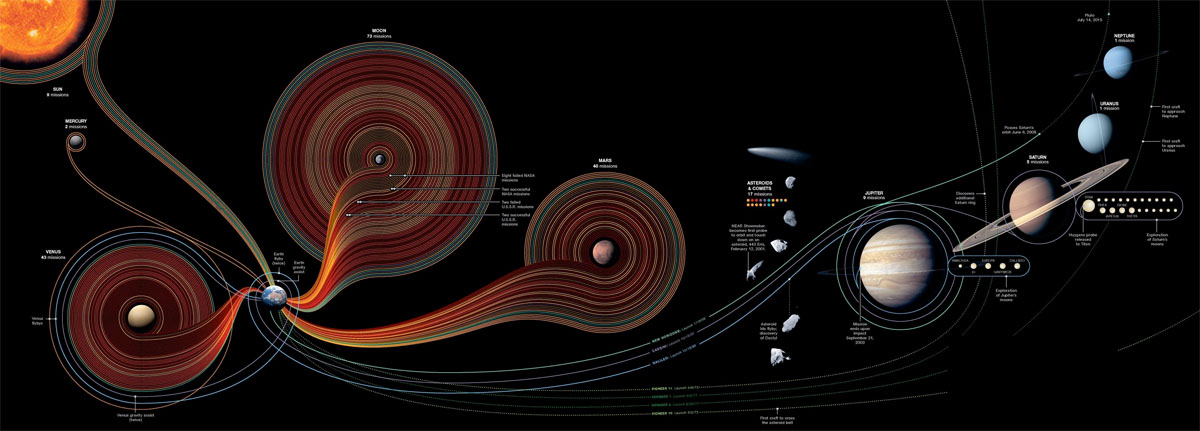
Траектории полета автоматических спутников за 30 лет к планетам и небесным телам Солнечной системы [10].
Эксперимент. Движение космический кораблей от Земли к планетам Солнечной системы
7. Коридоры движения космический кораблей от Земли к планетам Солнечной системы с учетом планетарного движения или геометрии

Коридоры движения космический кораблей от Земли к планетам Солнечной системы с учетом планетарного движения или геометрии. Т.о., определение Пространства, как геометрии или взаимного расположение сред и отношений тел их обобщения, в котором разворачивается событие для Макромира ближе к реальному положению явлений, чем определение по классической механике Пространства как движение тел в пространстве, являющимся евклидовым, абсолютным (не зависит от наблюдателя), однородным (две любые точки пространства неотличимы) и изотропным (два любых направления в пространстве неотличимы).
Данные экспериментальные исследования проведены для Макромира и основаны на каверзном восприятии [4] геометрии пространства. На основе каверзного восприятия можно показать Геометрию для микро- и мегамира. К этим важным категориям механики мы вернемся далее, когда включим Человека (наблюдателя) в архитектуру природы, введя понятие "мировой кварк", "рождение вселенной" и "целесообразность природного явления" через ноумен Человека, выполнив последнее требование для уточнения Механики [2].
ЗАКЛЮЧЕНИЕ. Проведено экспериментальное исследование определения Пространства для категории Психологической Механики 1) с исключением аксиоматических понятий и 2) исключения противоречия "теоремы о неполноте" (согласно которым всякая система аксиом начиная с определенного уровня сложности либо внутренне противоречива, либо неполна), 3) с рассмотрением реального механического движения, а не идеализированного, 4) с учетом схемы взаимодействия Пространство в механическом движении и Человек (наблюдатель), 5) с исключением критики научного агностицизма (время и пространство придумано для отражения Природы в науке и технике, не имея природного прообраза, поскольку познаваемый опыт неизбежно искажается идеализацией и логикой человека).
Далее мы рассмотрим "Законы кинематики в психологической механике и следствия. Применение для Макромира".
ЛИТЕРАТУРА:
- Психологическая механика. Psychological mechanics
- Древо Познания Механики. Tree of Knowledge Mechanics
- Психологическая механика. Человек и Пространство. Man and Space - 2013.
- , 2011.
- Риманова геометрия, А. Д. Александров, Ю. Ф. Борисов. Большая советская энциклопедия.
- Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971.
- Ландау Л. Д., Л и ф ш и ц Е. М., Теория поля, 7 изд., М., 1988.
- Рашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967.
- Евклидова геометрия — статья из Большой советской энциклопедии.
|